IQ Test Labs

Analytical reasoning

Diagrams

Diagrams display facts, rules and deductions and indicate what is true and false.

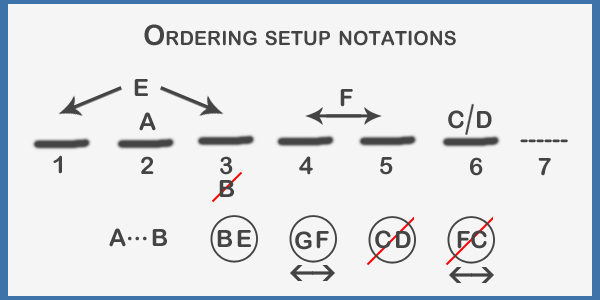
Ordering setup notations:

• 'E' is in either position 1 or position 3.
• 'A' is in position 2.
• 'B' is not in position 3.
• 'F' is in either position 3 or position 4.
• Either 'C' or 'D' can be in position 6.
• There are at least 6 positions, with a maximum of 7.
• 'A' is before 'B', and the number of positions is not known.
• 'B' is next to 'E' in that order.
• 'G' is next to 'F' in any order.
• 'C' is not left of 'D'.
• 'F' and 'C' are not next to each other in any order.

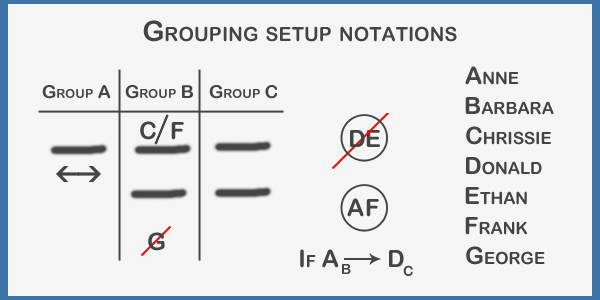
Grouping setup notations:

• The double arrow limits the first column to one item.
• The middle column and the right column contain at least two items.
• 'D' and 'E' cannot belong to the same group.
• 'A' and 'F' belong to the same group.
• 'G' is definitely not in Group B.
• If 'A' belongs to Group B, then 'D' belongs to Group C

Deductions

• Deductions are most likely to be made through the examination of statements which share common elements.
• Deductions are statements about what must be true or false, that were not stated explicitly.
• For example if an apple is heavier than a pear, and the pear is heavier than an orange, the apple can be deduced to be heavier than an orange, even thought that information was not specifically given.
• Figure out as many deductions as possible before starting the questions. This will save time by not having to go back for each question, in order to make the same deductions all over again.
• Elements/items that take up permanent positions/spots in diagrams are instrumental in making deductions.

---

---

Equivalent rules

An equivalent rule is one of the fastest way make a deduction.

Equivalent rules are often derived from conditional rules.

Example 1

If A lives with B, then C lives with D.

The conditional rule, is itself a deduction i.e Once it is affirmed that A lives with B, it can deduced that C lives with D.

Logically equivalent rule: If it is affirmed that C does not live with D, it can be deduced that A does not live with B.

Note: C could live with D, even if A doesn't live with B.

Example 2

If A then B.

Equivalent rule: If not A then not B.

Therefore:

If Ann is sleeping, then Barry is sleeping.

If Anne is not sleeping, then Barry is not sleeping.

Example 3

If not A then B

Equivalent rule: If not B, then A.

Therefore:

If Anne is not sleeping the Barry is sleeping.

If Barry is not sleeping, then Anne is sleeping.

Repeats

It is often possible to make deductions from elements that appear in more than one rule.

Example:

Rule 1: Game A is to be played before game B.

Rule 2: Game B begins on an odd hour.

Deduction: Game B can only be played at 3 p.m or 5 p.m. 1 p.m is ruled out because it has to be played after game A.

Ordering setups

Common ordering setups:

• Prioritising tasks in a workday.
• Determining the order in which employees take their summer vacation.
• Scheduling sports games in a league.
• Seating arrangements around a circular table.
• Assigning yoga instructors to classes in a yoga retreat.
• Ranking movies, from 5 stars to 1 star.

Ordering setup questions:

Grouping setups

Order doesn't matter in groups. If A and B both belong in Group C, it doesn't matter if A comes before or after B.

Common grouping setups:

• Determine which of three sports each of 8 people will play on a cruise ship.
• Determine whether each of 24 students are in the football team or not in the football team.
• Determine whether each of 8 employees will work morning shifts, afternoon shifts, or both.
• Determine which 4 of 8 students are in the debate society and which 4 are in the poetry club.

Grouping setup questions:

Mixed setups

In mixed configurations (both ordering and grouping) the rules in the diagram should clearly reflect which of the two they are referring to.

Common mixed setups:

• Determine which sports event twelve children will participate, and in which sports field. (group + group)
• Determine which sports event twelve children will participate, the house group, and the sports field. (group + group + group)
• Determine which sports event twelve children will participate, the sports field, and the day of the week. (group + group + ordering)
• Determine which day five employees that work in two different departments will take their day off. (group + order)
• Determine which eight athletes will compete in the track event and the lane order. (group + order)

Keywords

Take special note of key words that define relationships between elements.

Examples include minimum, maximum, exactly, always, never, at least, only, can/cannot be, possible/not possible.

Outside knowledge

Disregard and brush aside knowledge you may have about a particular topic in a passage. The passages have provide sufficient facts, and all outside knowledge is unecessary.

Rule/choice elimination

It can sometimes be helpful to eliminate choices based on rules. Eliminating choices that don't adhere to a specific rule helps avoid situations where all choices are consecutively checked against all rules.

Scenarios

Scenarios can be time saving when groups, and not elements, are restricted to either two or three situations that conform to all stated rules.

Example:

Suppose we want to know the order of appearance of six actors in a movie, A,B,C,D,E,F

We know that A comes before D, and that there are three actors between them.

This leaves only two possible scenarios.

First scenario: A _ _ _ D _

Second scenario: _ A _ _ _ D

This is a great way to eliminate choices. Furthermore, an extra rule, such as D appears before F would eliminate the second scenario since D cannot be last.

---